これ。
手紙にスタンプをおして投函するだけのゲームです。全6ステージ。https://t.co/BMJn5CUzff
— Yusuke Endoh (@mametter) 2022年11月8日
以降には答えも載せているので、まずは自力で解いてほしい。 Stage 3までは人力で、Stage 5まではプログラムを書けば解けると思う。
プログラムを書いて解く
Stage 4以降は人力では無理だったので、プログラムを書いた。 ソースコード。
どんなアルゴリズムを使っているか。
反復深化法
このパズルは、基本的には、クリアしないままいくらでも続けることができてしまう。 同じ状態がループしたり、あるいは上段か下段がいくらでも長くなったりする。 単純に再帰で深さ優先に探索すると、クリアできない選択肢を掘り続けてしまう。 幅優先で探索しようとすると、メモリが大量に必要になる。
そこでおすすめなのが反復深化法である。 まずは、最大深さ(最大手数を)1に制限して、深さ優先で探索をする。次に最大深さを2に制限して、3に制限して……と徐々に深くしていく方法。 答えが見つけられなかった最大深さの探索が無駄に思えるかもしれないが、意外とそうでもない。 例えば、1手に3通りの選択肢があって、4手で解けるとしたとき、いきなり最大深さを4にしたときは、34=81ノードの探索が必要になる。 反復深化で1手づつ最大深さを増やしていったときは、31+32+33+34=120ノードである。 そんなに大きくは変わらない。 ……というのが教科書的な説明だけど、この問題は置けないピースが多くて、実際には1手あたり3通りも無いので、けっこう無駄になる。 1手ずつ増やすのではなく、もっと段階を粗くするのも良いかもしれない。
ピースの個数の比を求める
このパズルは先のステージに行っても、ピースの個数は3個のままである。 そして、上段に流した封筒の個数と、下段に流したハンコの個数は等しい。 上段のハンコと下段の封筒の個数も同様。
各ピースを何個使うかを3個の変数で表し、等式が2個あるので、変数を2個消せる。 ある1種類のピースの個数で他の2種類のピースの個数が表せる。 つまり、ピースの個数の比が分かる。
反復深化で、使うピースの合計数を決めれば、各ピースを何個使うのかも決まる。 あるピースを使い切ったら、その時点で探索を打ち切ることができる。 これが枝刈りとして優秀だった。
左右を逆にする

上がstage 5の問題、下が各ピースの左右を逆にしたもの。
こうしても本質的には同じ問題である。 ポストに入って消えるのではなく、残しておいて、上下段の右端が揃ったらクリアという問題だと考えると分かりやすいかもしれない。 ピースを使う順番は逆になる。
あるいは、ピースの左右を逆にするのではなく、ポストを右に置いて、左から右に流す問題と考えても良いかもしれない。
本質的には同じ問題だが、探索の難易度は変わる。 他のステージは試していないが、stage 5と6は逆のほうが探索が速くなった。
今後必須になるピースを考える
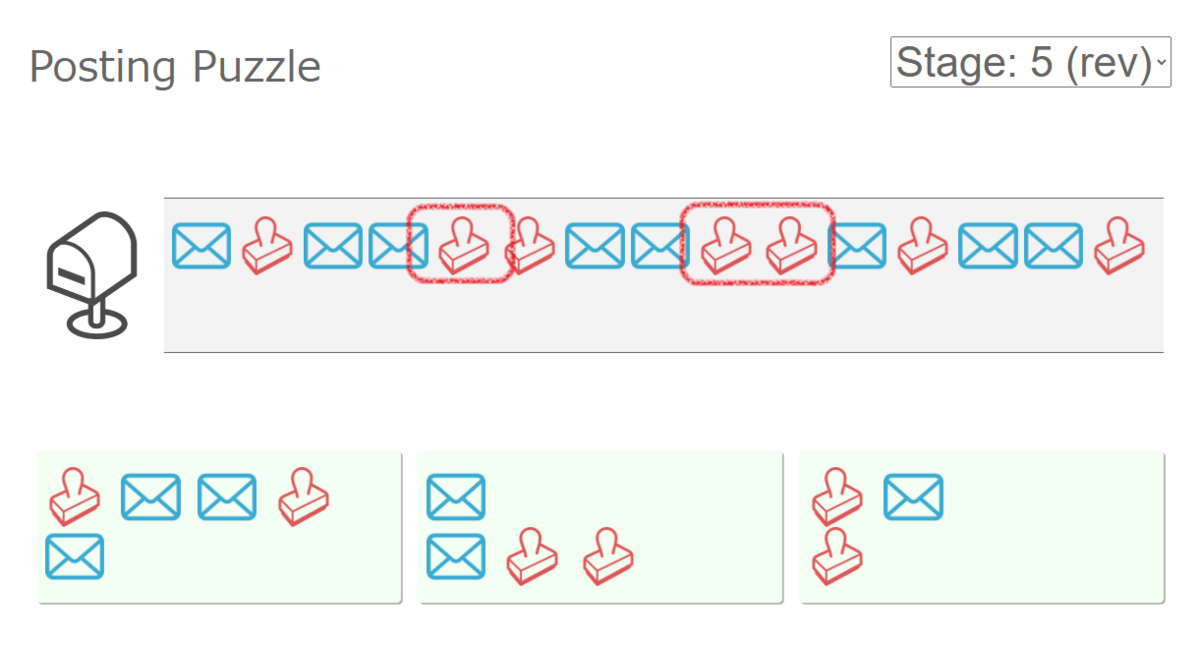
Stage 5の左右を逆にした問題で、赤枠で囲ったスタンプに注目する。 中央のピースにも封筒はあるけれど、中央のピースはここには置けないので、ここでは必ず左のピースを使うことになる。 この時点で将来左のピースをいくつ使うのかも考慮に入れ、「ピースの個数の比を求める」の枝刈りをすることで、より早期に枝を刈れて速くなる。
上段か下段が長くなりすぎたら打ち切る
Stage 5はこれで解けた。 ここまでに出てきた手法は全て、答えがあるならば必ず見つけるし、(反復深化を1手ずつ増やせば)最短手数の解法が見つかる。 解けないことが確定した時点で枝刈りをするので。 上段か下段が長くなりすぎたらそこで探索を止めるのは、解けないことが確定する前に枝刈りをするから、あるはずの答えが見つからないことがあるし、答えが出てきても最短手数とは限らない。 できれば最短手数だと確定できる答えを見つけたかったが、諦めた。
答え
ピースは左から順番に0, 1, 2としている。
Stage 1
001
最短3手。
Stage 2
2012
最短4手。
Stage 3
0200211
最短7手。
Stage 4
022001022210002022110101120222201000012102211202101002202121100102111211211
最短75手。
問題はこれ。

先のステージでもピースの中の封筒やスタンプはそんなに増えない。それなのに、これだけ手数が増えるとは驚き。
Stage 5
1211212112111011212120121121121011101110112012120121201210112101121011201211201211201210112121011101 0112012112112012120012101110111010112201120121201212001101101011210112201201200121120110122122011101 0120111101101200101101201202001201022021201121012112011101012120011220121101121201211210112121120121 1211101011101110120012120121202011210112210121120121112011101011101210121200121201120112201122110101 1011011121200120120110112201010120110120010120200220
452手。 最短かどうかは分からないが、まあ、たぶん、最短じゃないかな。 驚きの長さ。
解いているときにどんなことになっているのか気になりますよね。 動画を撮っておきました。
動画を撮って気が付いたけど、下段が一旦短くなって、また長くなる。 個数の比からピースの個数を求めて……の枝刈りは、上段か下段が長すぎるのを制約するという役割もある程度兼ねている。 使うピースが偏れば、上段と下段の個数も偏るので。 それなのに、「上段か下段が長くなりすぎたら打ち切る」が効いたのは、下段が一旦短くなるからかもしれない。
Stage 6
解けません。 いや、解けないとか、あるいは未解決問題だとか、ありえると思ったんだよな……。 でも、「もしかしたら解けるかも」で随分と時間を溶かしてしまった。 証明は後述。
ポストの対応問題
このパズルは「ポストの対応問題」の一種である。
ポストの対応問題は、例えば、次の各ピースを何回使っても良いので、上段と下段を一致させよという問題。
0 1 2 ab bb c ba b bc
答えの一例として、 1002 と並べると、上段も下段も bbababc になる。
ポストの対応問題の文字を a と b の2種類にし、下段の文字の a と b を入れ替えると、Posting Puzzleになる。
「Posting Puzzle」という名前(と郵便ポストに入れるというアイデア)は、このポストの対応問題からでしょう。
ちなみに、ポストの対応問題のポストは、郵便ポストではなく人名である。
ポストの対応問題は、決定不能問題(その問題を解くようなプログラムが存在しない問題)として知られている。 Stage 6のような解けない問題があると言っているわけではなく、解けるかどうかを判定するという問題が解けない。 「そんなの証明できるの?」と思うかもしれないが、証明されている。 問題の表現力が高く、もし解くプログラムが存在するならそのプログラムを埋め込んだ問題が作れて、なんやかんやできる……と私は理解している。
決定不能問題に興味があるなら、このサイトがおすすめ。
で、文字種が2種類のポストの対応問題で、ピースの数やピースの幅が少ないものについて、解けるかどうかや最短手数を網羅的に調べていた人達がいた。
Stage 4は、ピースが3個で、各ピースの最大幅が3の最も手数の掛かる問題である。
Stage 5は、上のリストには載っていないが、Internet Archiveに残っているページに載っていた。
ピースが3個で、各ピースの最大幅が4の最も難しい問題の候補だろうか。 この時点で、452手で解け、340手以内では解けないことが分かっているっぽい。 最短手数が何手かはまだオープンな問題かもしれない。
Stage 6は、この文献に解けないことが証明されたと書かれていた(ここでの「solved」は解けないことが示せたの意)。しかし「Unpublished manuscript」。
https://webdocs.cs.ualberta.ca/~mmueller/ps/jea.pdf


証明が気になるけど、publishされたmanuscriptが見つからない……ということで、Rahnさんにメールで訊いた。
20年前の話だし、スルーされるか、「もう忘れたよ」かと思ったけど、すごく丁寧に教えてくれた。 ありがとうございます。
メールの文章や、送ってもらった論文を転載するのは憚られるけど、証明自体は、公開されているRahnさんの博士論文の42ページにも載っているとのこと。 ドイツ語だけど。
https://publikationen.bibliothek.kit.edu/1000009979/614948
概略。

ピースの左右を逆にした問題を考えると、AかBのパターンが必ず出てくる。 そして、AかBのパターンの後には、必ずAかBのパターンが出てくる。 よって、このパターンは消えることが無く、この問題は解けない。
「AかB」という2種類のパターンがあるのがミソである。 BBBBBB...やBAAAA...などがありえるので、AかBどちらか一方のパターンのみを考えていては、解けないという証明はできない。 そう、1個のパターンを使う方法は思いついていたんだよな……。 でも、色々なパターンを試してみても、どうしてもパターンが消えてしまうパスがあって困っていた。 Stage 6を自力で解けたり、解けないことを証明したりできなかったのは悔しいが、証明が分かってすっきりした。