HTR Subsetsのほうが簡単なので。簡単な分、U2の回数も考慮して状態を分けられるので、その辺をメモしておく。
Hyper-Parityとは
この辺を参照。 要は、U/D面の状態とF/Bの状態の組み合わせについて、どのような遷移が可能かまとめるとHyper-Parity Mazeになり、偶奇が合うようにSolvedな状態に向かうと、コーナーのHTRが完了する。
HTR Subsetsとは
HTR Subsetsでは、0c3や4b2のような3文字で状態を表す。 先頭の2文字には、0cと4a、4b、2cがあり、それぞれHyper-ParityのF/B面のSolved、One Face、Bars、One Barに対応している。 先頭の数字はバッドコーナーの個数。 2文字目の英字は、バッドコーナー4個のOne FaceとBarsを区別するためだろう。 末尾の数字はQT数。 QT数なのでQTの偶奇の情報も含まれており、Hyper-Parityのように各状態に偶数と奇数が別にあるわけではない。
無理矢理分けているようにも思えるが、例えば2c4に含まれるある状態からは2c3に遷移できるが別の状態からは遷移できないというようなことは一切無い。 もしかすると、U/D+F/B=Bars+Barsが3個の状態に分かれたりするHyper-Parityよりも本質的なのかもしれない。
HTR Subsetsの判別
Hyper-ParityのF/B面の状態とQT数なので、Hyper-Parityを知っていれば、HTR Subsetsのどの状態かを判別することはできる。 Hyper-Parityの各状態について、偶奇別のQT数は次の通り。

しかし、もっと覚える事が少ない方法がある。
まずはF/B面の状態から、先頭の2文字を特定する。 その後、次のようにしてHTR Subsetsの状態が分かる。
0c
Hyper-ParityのU/D面がSolveかどうかを、F/B面とR/L面についても見る。 Solvedなものが0個ならば0c4、1個ならば0c3、2個になることはなく、3個ならば0c0。 BLDトレースは不要。 なぜこれでパリティを含めて判別できるのかが分からない……が、便利。
2c
バッドコーナーを2個を頭の中で入れ替えて、0cと同様のことをする。 0個ならば2c3、1個ならば2c4、3個ならば2c5。 揃っている個数とQT数が0cとは逆になる。
4a, 4b
BLDトレースでQT数の偶奇を求める。 また、normal方向とinverse方向で4aと4bのどちらになるかを調べる。 バットコーナーの側面色を見て、側面色が同じものをペアにしたとき、ペアが1組なら逆方向は4b、0組か2組ならば4a。 どちらも4aならばQT数は1か2、4aと4bならば3か4、4bと4bは5か6……ではなく、2か5。
HTR Subsetsの遷移
下図のように遷移する。
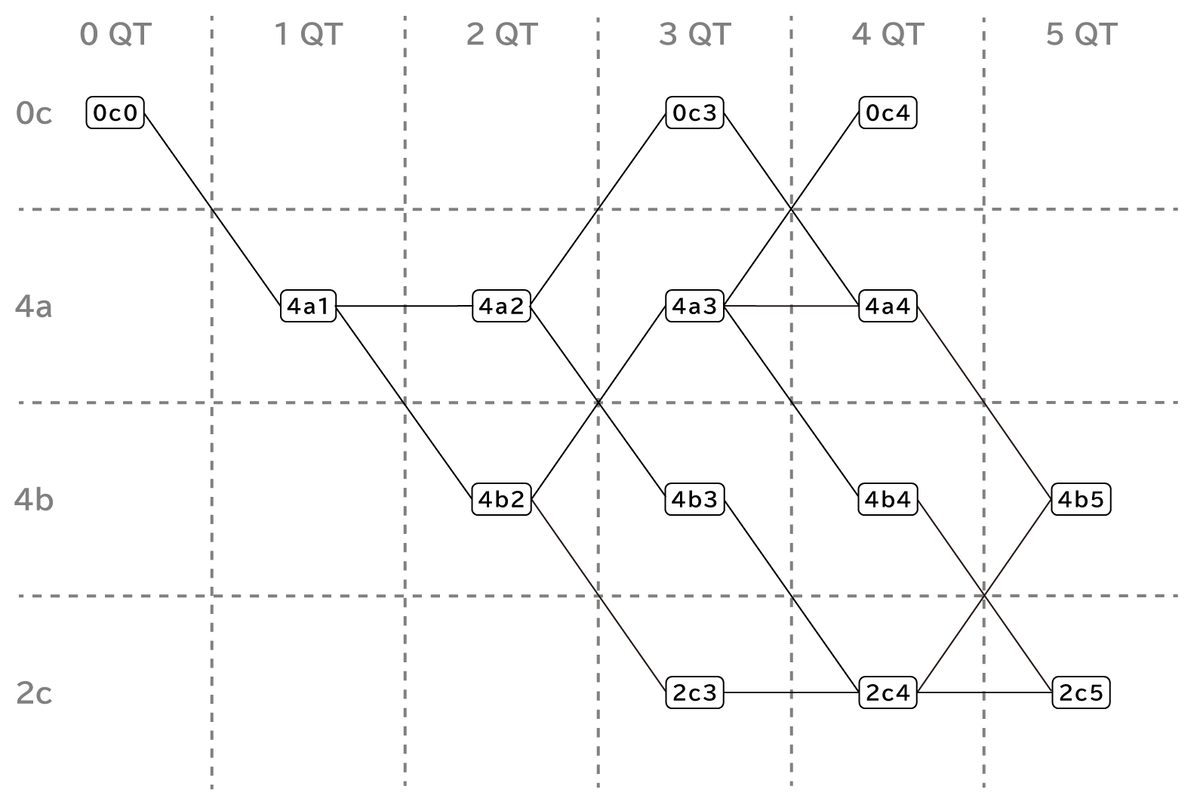
ところで、QT数が同じだからと言って、HTR完了までの手数の期待値が同じとは限らない。 例えば、2c3 → 4b2 → 4a1 → 0c0 は最短5手でHTRが完了する。 一方、0c3 → 4a2 → 4a1 → 0c0 は途中に2回のU2が必ず入り、最短でも9手。
HTR SubsetsではU2で遷移するものは同じ状態として扱うけれど、これを別にすればより正確になるのでは? と思ってやってみた。 こうなった。

https://gist.github.com/kusano/edc2607bb41d97d4592086809bbc993c
+ と - はHTR完了までが近いかどうか。
その後の a と b は区別するためだけで特に意味は無い。
横軸をQT(U/U')ではなく、U2も含めた回数にするとこうなる。

基本的には最短手数を目指すことになるので、縦方向の遷移は省略して良いだろう。 また、4a3+aと4a3+bが分かれていることで、0c4 → 4a3 → 4b4にはU2が必要なことが分かるが、こんな遷移はしないので、4a3+aと4a3+bはまとめてしまって良いだろう……など整理すると、こうなった。

これを覚えれば良いのではなかろうか。
解き方
上の図にしたがって解くとき、HTR Subsetsの各状態で行うこと。
多くの状態は、単にF/B面を目指す状態にすれば良い。 そのような状態は次の通り。 例えば、4b3は、4aにすると必ず目指したい4a2になる。4a4にはならない。
| from | to |
|---|---|
| 0c4 | 4a3 |
| 4a1 | 0c0 |
| 4a2 | 4a1 |
| 4a4 | 4a3 |
| 4b3 | 4a2 |
| 4b4 | 4a3 |
| 4b5 | 2c4 |
| 2c3 | 4b2 |
| 2c5 | 2c4 |
遷移する方法は次の通り。
- 0c → 4a
- U/U'で常に遷移する
- 4a → 0c
- バッドコーナーをU面かD面に集める
- 4a → 4a
- バッドコーナーをFLとBR、もしくはFRとBLの対角線に集める。U/U'でU面のコーナーがバッドかどうかが切り替わるので4aのまま
- 4a → 4b
- バッドコーナーをU面とD面に2個ずつにする
- 4b → 4a
- バッドコーナーをU面とD面に2個ずつにする
- 4b → 2c
- バッドコーナーをU面とD面で1個と3個に分ける
- 2c → 4b
- バッドコーナーをU面とD面に1個ずつにする
- 2c → 2c
- 2個のバッドコーナーをU面かD面のどちらか一方に集める
F/B面の状態だけ見ていると悪い方向にも行く可能性がある場合が厄介。
0c3
4a2に行きたいが、単に4aにするだけだと4a4になりうる。
バッドコーナーをU面とD面に2個ずつに分けつつ、U/D面の状態がSolvedなら、U/D面はU面の色を全て同じにしてSolvedに行くか、対角を同じ色、隣接を別に色にしてSlashesに行くか。 バーにしてBarsに行くのがNG。 U/D面がBarsなら、U面とD面に2個ずつにしてSolvedに行く。 1個と3個にしてBar/Slashに行くのがNG。
4a3
バッドコーナーをU面とD面に2個ずつにして、4b2に行きたい。 4b4になる可能性がある。
U/D面がSolvedの場合は、遷移先がSolvedかBars(BB1)(バッドコーナーのU/D面の色が2色)はOK。 Bars(BB2)(バッドコーナーのU/D面の色が全て同じ)がNG。 Bar/Slashならば、遷移先がBar/SlashがOKで、BarsがNG。
4b2と逆で、ただし、U面が全て同じ色はOKと覚えるが良いか?
4b2
4a1に行きたいが、4a3になりうる。
バッドコーナーを2個ずつにして、U/D面がSolvedならバーを違う色、Barsなら同じ色、Bar/SlashならU面色をU/D面に1個と3個に分ければOKらしい。
2c4
2c3に行きたいが、2c5になりうる。
バッドコーナーをU面かD面に集めてUかU'を回した後、バッドコーナーを入れ替えて、U/D面がSolvedになってなければOK。
2cへの遷移は、2c3か2c5になる。 判別法のところで見たように、2c3ならSolvedな軸は0個、2c5なら3個なので、どれか1面を見れば良い。 U/D面が簡単。
NISS
NISSのスイッチでどの状態に切り替わるのかを調べてみたら面白いかと思ったが、特に面白いことは無かった。

4a3と4b3、4a4と4b4が切り替わる以外は、同じ状態の中のどこかに切り替わる。 QT数もバッドコーナーの個数も変わらない。 Normal方向で最後に回した180度回転は、inverse方向では初期状態からの180度回転になり、これはHTR的な状態を変えないので、そりゃそうか。 4a3と4a4で次の状態に進むためにU2が必要ならスイッチすると得。 それ以外のU2が必要なときは、得するかもしれないし、しないかもしれない。
NISSといえば、例えば、
(A U) B U2 (C U') D U // HTR
このように解いたとき、これは次のようにも解ける。
(A U C U') B U2 D U // HTR B U2 D U (A U C U') // HTR
NISSの括弧の中は、最後はまとめて逆手順を付け足すことになるので、どこにあっても同じ。 しかし、4aと4bが絡むようなときは、HTR subsetsの推移としては別になるはず。 この辺何か面白い話はないだろうか。
Hyper-ParityのU/D面とF/B面の状態は全く同じという話
乗り換えようとしているので、最後に。 何となく似ているようだが、似ているどころか全く同じである。
コーナーを、(UBL, UFR, DBR, DFL), (UBR, UFL, DBL, DFR) の2グループに分ける。 グループ内のキューブが同じグループ内のどこかにあるときグッドコーナーになり、別のグループの位置にあるとバッドコーナーになる。
キューブをこのように塗り分けて、赤を赤のところに、緑を緑のところに配置すると、F/B面がSolvedの状態になる。 これは、赤をU面色、緑をD面色と見なすと、U/D面のSlashesと同じ配値。 U/D面のSolvedの配置にすると、F/B面の状態としてはOne Faceになる。 BarsならBars、Bar/SlashesならOne Bar。
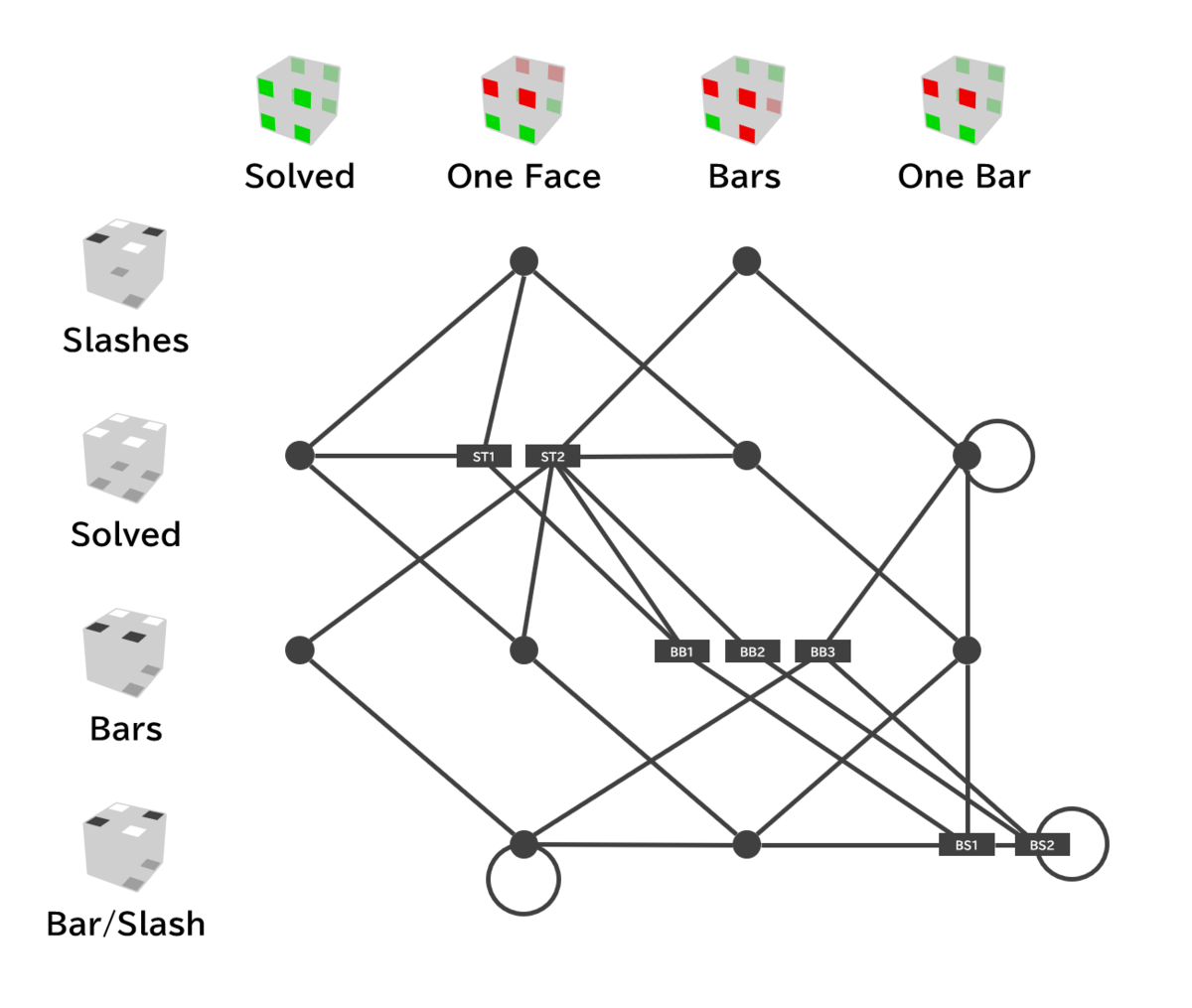
この図は、左上と右下を結んだ直線に対して微妙に線対称になっていないが、これはST1やST2など複数の状態があるものを横に並べているからで、これらを画面手前と奥の方向にでも並べれば、この図は完全に線対称になる。
